Channel Coding for High Speed Communication
The fundamental problem of communication is that of sending information from one point to another (either in space or time) efficiently and reliably. Examples of communication are the data transmission between a user and a mobile cell tower, between a ground station and a space probe through the atmosphere and free space, the write and read of information on flash memories and hard drives, as well as communication between servers in a data center through optical interconnects. The transmission over the physical medium is subject to noise due to amplification, distortion, and other impairments. As a consequence, the transmitted message may be received with errors.
To reduce the probability of error, Claude E. Shannon showed in his landmark work that with the use of channel coding, the error probability can be made diminishingly small. The principle of channel coding is very simple: to introduce redundancy in the transmitted sequence in a controlled manner such that it can be exploited by the receiver to correct the errors introduced by the channel. This is provided that the rate of the channel code (which determines the overhead added for data protection) is below a quantity called the channel capacity, which is a fundamental limit for any channel.
Today, many channel codes used in practical systems are based on the concept of Low-Density Parity-Check (LDPC) codes. This is mostly due to their good theoretical foundations and the availability of a very fast and simple decoder that can be easily parallelized in a VLSI implementation. LDPC codes were already introduced in the 1960s, but then forgotten due to their large perceived complexity for that time. After the invention of Turbo codes in 1993, a sudden interest in iteratively decodable codes led to the rediscovery of LDPC codes in the 1990s. In the years that followed, a thorough theoretical understanding of LDPC codes was established and LDPC codes were adopted in numerous applications (e.g., WiFi 802.11, DVB-S2, 10G Ethernet (10G-BaseT), 5G mobile communications, and many more).
Channel coding for high-speed communications
In high speed communications over long distances (e.g., optical fibers, optical submarine cables, microwave radio links for connecting remote antenna sites, and many more), we would often like to maximize the coding gain (and hence the data throughput) with still manageable decoding complexity. If a very large coding gain shall be achieved, LDPC codes are still a good choice due to their well-understood error correction properties and the availability of a massively parallel decoder. However, we would like to increase the coding gain even further.
About two decades ago, LDPC convolutional codes were introduced. These codes superimpose LDPC codes with a convolutional structure. The initial goal was to combine the advantages of both convolutional and LDPC codes and the resulting codes were called LDPC convolutional codes. A similar idea was already pursued in the late 1950s and early 1960s with the concept of recurrent codes. The full potential of LDPC convolutional codes was not realized until a few years later, when it was realized that the performance of some LDPC convolutional code constructions asymptotically approaches the performance of optimum maximum likelihood decoding. For investigating this effect, a slightly modified construction called "spatially coupled codes" was introduced. In the following, we restrict ourselves to using this latter term. The main advantage of spatially coupled codes is that very powerful codes can be constructed which can be decoded with a simple windowed decoder. Therefore, spatially coupled LDPC codes (SC-LDPC Codes) can be considered prime candidate for increasing the coding gains in high-speed communication systems.
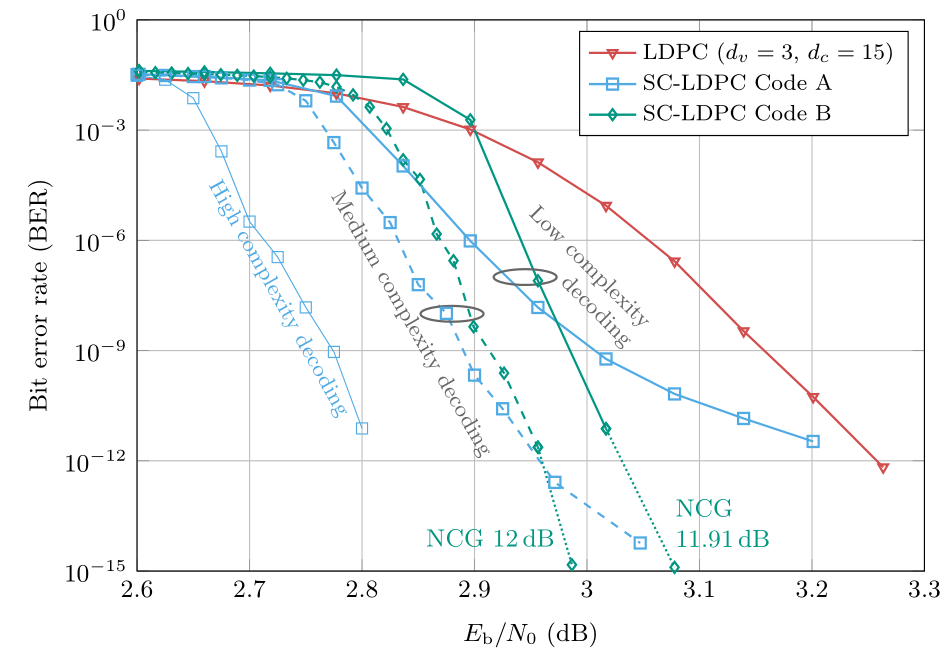
The following picture shows the bit error rate obtained by two SC-LDPC codes compared with a conventional LDPC code often used if low error rates are targeted. All codes have the same rate of 0.8, which corresponds to an overhead of 25% for parity bits. With low-complexity windowed decoding, which has roughly the same complexity than standard LDPC decoding, we can already achieve a significant gain compared with the LDPC code. The main advantage of SC-LDPC codes is that they are future-proof. Increasing the complexity will lead to larger coding gains. This favors their use in communication standards, such that with a given standardized and backwards compatible system, larger gains will be available if the VLSI performance increases in the future or if better decoders become available. We can also note that at a bit error rate of 10-15, we are within 1dB of the Shannon limit with an implementation that uses finite precision arithmetic.
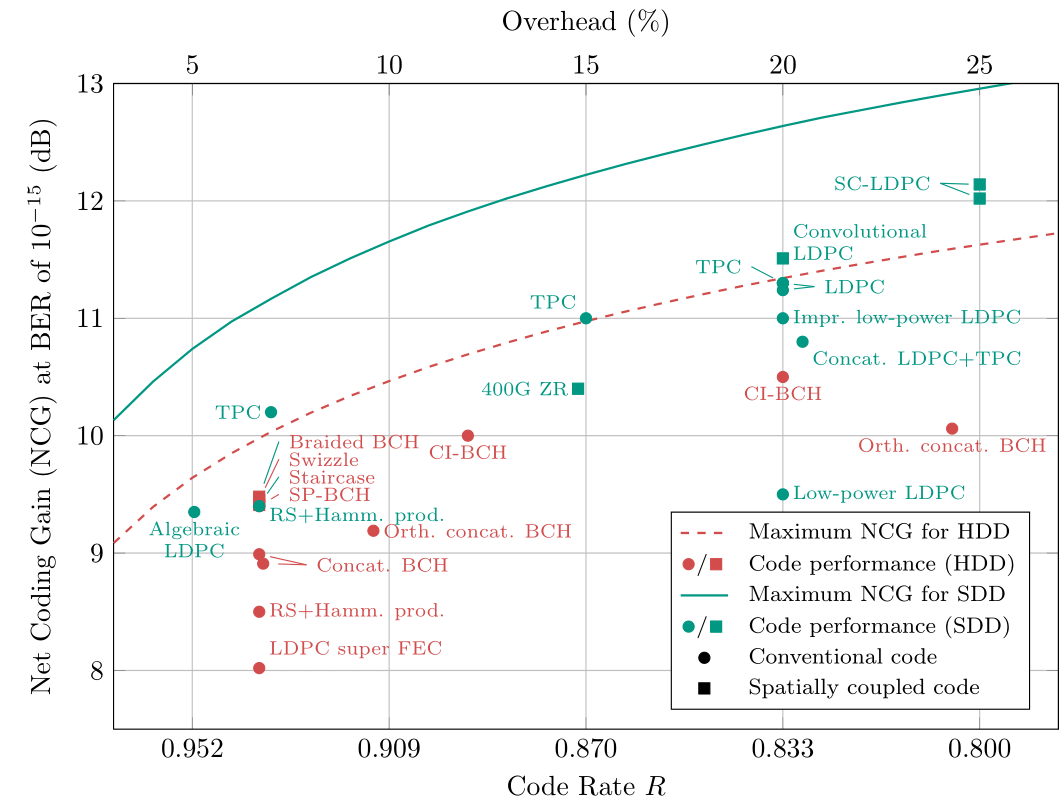
The following picture shows the net coding gains of some channel coding schemes used in optical communication systems, a prime example of a high-speed communication system. We distinguish between channel codes with hard-decision decoding (HDD), which are usually designed for low-complexity transceivers and channel codes with soft-decision decoding (SDD), which are usually designed for high-performance transceivers. Square markers indicate the schemes where spatially coupled codes are used. The most powerful coding schemes that are currently being used belong to the class of spatially coupled codes. In particular the SC-LDPC Codes A and B shown above deliver best in class performance.
Channel coding research at CEL
At CEL, we carry out fundamental research on channel coding for high-speed communication systems. We intend to develop new coding schemes suited for low-complexity decoding and delivering best possible coding gains. We aim at low error floors and consider peculiarities of the transmission system, e.g., optical channels, or microwave backhaul channels. Besides spatially coupled codes, we continue to assess other possible coding schemes depending on the application.
Related literature
- V. Aref, N. Rengaswamy and L. Schmalen, "Finite-Length Analysis of Spatially-Coupled Regular LDPC Ensembles on Burst-Erasure Channels", IEEE Transactions on Information Theory, vol. 64, no. 5, pp. 3431-3449, May 2018 [IEEE Xplore] [preprint on arXiv]
- L. Schmalen, V. Aref, J. Cho, D. Suikat, D. Rösener, and A. Leven, "Spatially Coupled Soft-Decision Forward Error Correction for Future Lightwave Systems", IEEE/OSA Journal on Lightwave Technology, vol. 33, no. 5, pp. 1109-1116, March 2015 [IEEE Xplore]
- L. Schmalen, D. Suikat, D. Rösener, V. Aref, A. Leven, and S. ten Brink, "Spatially Coupled Codes and Optical Fiber Communications: An Ideal Match?", IEEE Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Special Session on Signal Processing, Coding, and Information Theory for Optical Communications, Stockholm, Sweden, June 2015 [IEEE Xplore] [preprint on arXiv]
- A. Leven and L. Schmalen, "Status and Recent Advances on Forward Error Correction Technologies for Lightwave Systems", IEEE/OSA Journal on Lightwave Technology, vol. 32, no. 16, pp. 2735-2750, Aug. 2014 [IEEE Xplore]

