Channel Coding: Graph-based Codes

The course focuses on modern graph-based methods for error correction coding (channel coding) that have been brought into practice in the past few years and that achieve the capacity limits postulated by Shannon. For this purpose, known techniques have to be extended and new methods have to be learnt additionally. The lecture introduces the theoretical limits and follows with a discussion on the basic concepts of channel coding,including block codes. Based on this, modern error correction methods like LDPC codes, spatially coupled codes, and Polar codes are treated in depth. The lecture ends with a view on the application of channel coding in classical and distributed storage scenarios and in computer networks. Many of the applications are illustrated with example implementations in software (python/MATLAB).

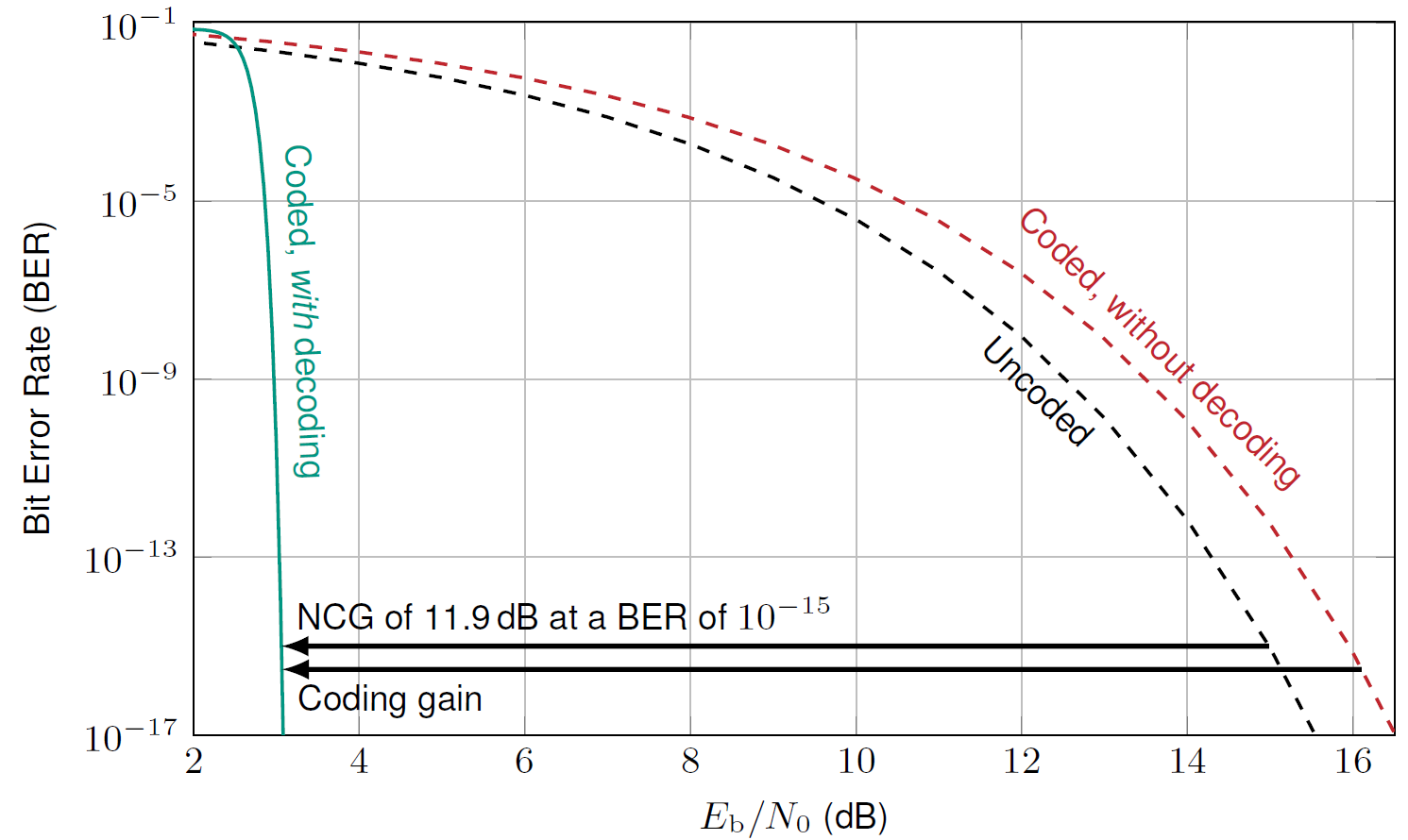
The course starts by introducing the necessary fundamentals of coding theory and information theory, to understand the fundamental limitations of what channel coding can achieve and where it will not be useful to employ channel coding. We introduce abstract and simplified channel models and compute their capacity limits, determining how much data can be transmitted over a channel and how coding can be used to closely approach these limits. The following picture shows how a modern coding scheme as it is used for instance in fiber-optic communications can yield net coding gains of around 12 dB at extremely low error rates (corresponding to 10 bit errors per day at a data rate of 100 Gbit/s).

Following the fundamentals, we introduce the concept of linear block codes, which form the basics of all modern coding schemes. After defining and describing the different ways of describing linear block codes, we introduce a special class of linear block codes, called Low-Density Parity-Check (LDPC) codes. These codes are defined by a sparse parity-check matrix, containing a significantly larger number of zeros than ones. An example of such a matrix of size 150x300 is shown here:

where the ones are shown as small dots. We also introduce an alternative representation of this matrix using graph theory, the so-called Tanner graph. An example Tanner graph is given by

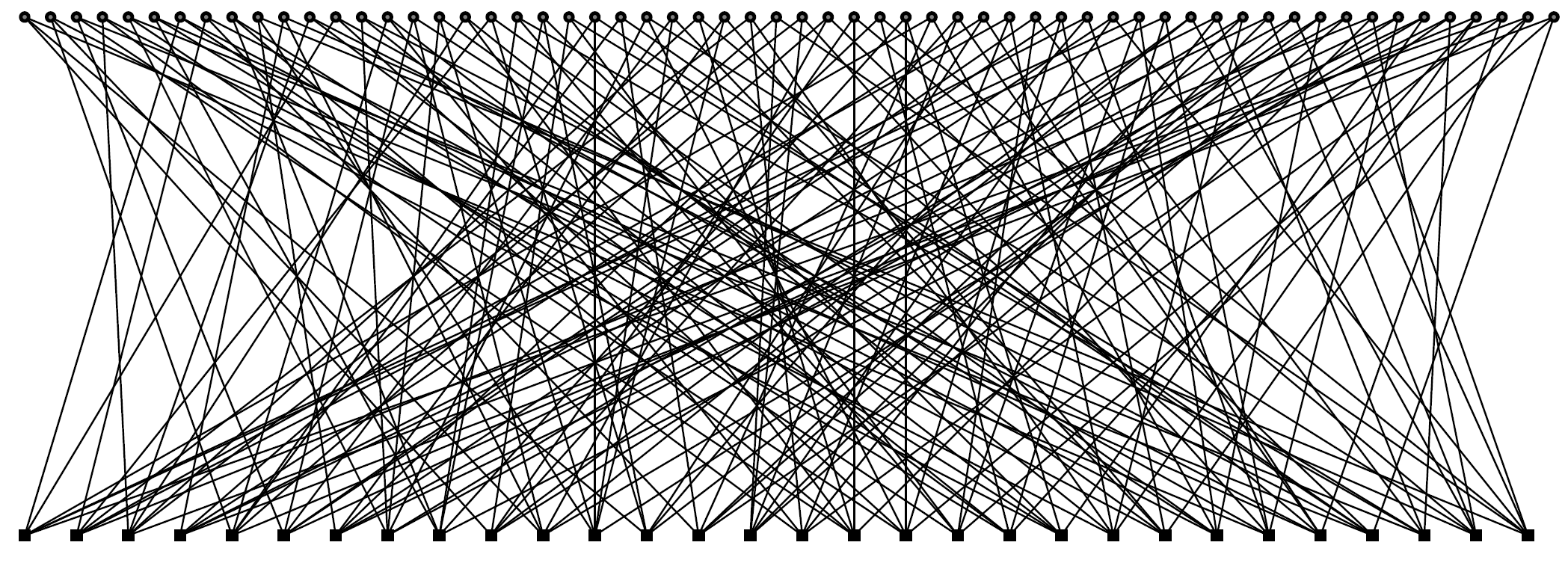
The Tanner graph forms the basis for a very efficient decoding algorithm, the sum-product algorithm, which in its variant is employed in almost any modern communication device (e.g., mobile phones, WiFi devices, etc.). The basic sum-product algorithm is given by

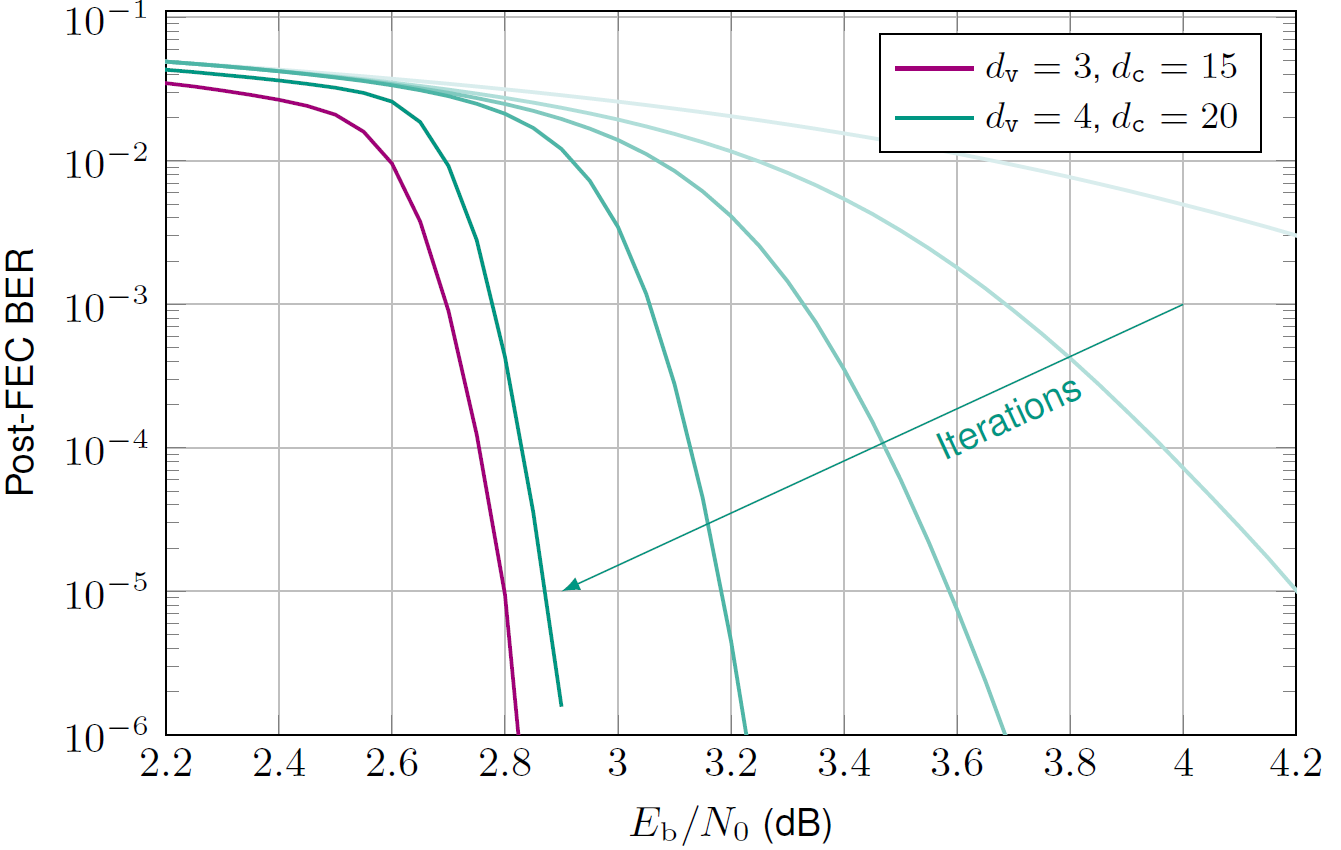
We will look at different simplifications of the decoder focusing on low-complexity implementation on digital electronics. The sum-product algorithm is an iterative algorithm that improves the bit error rate performance with increasing number of iterations as illustrated in the following figure. 

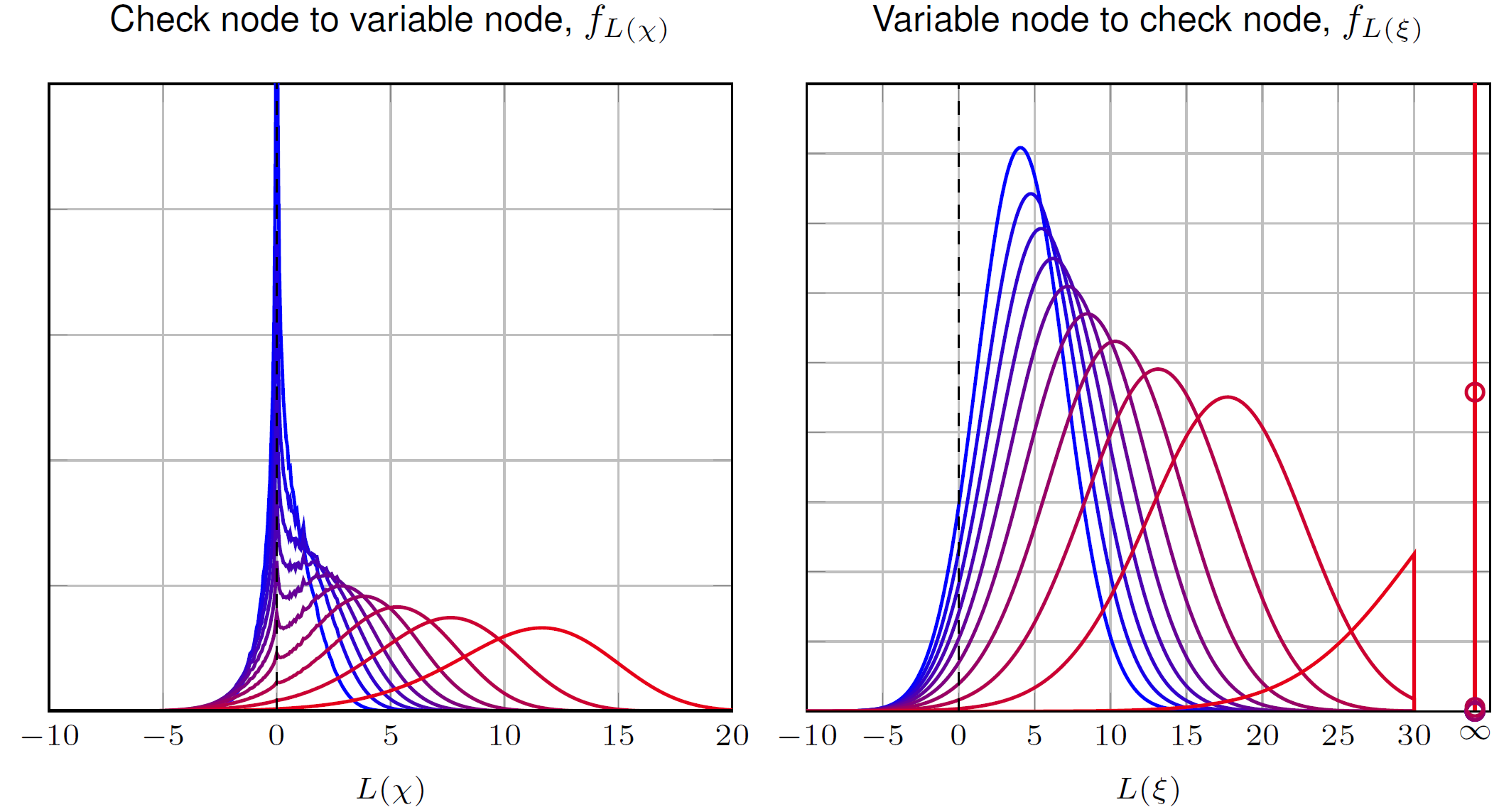
When simulating codes, we observe that different code configurations yield different decoding performance. Hence, the sum-product decoder forms the basis for an in-depth analysis of LDPC codes to assess which configuration leads to which performance. We will derive tools for optimizing LDPC codes by evaluating their asymptotic performance using simple numerical tools. We start with the binary erasure channel, where a very simple analytical expression exists for assessing the performance that is illustrated in the following figure:

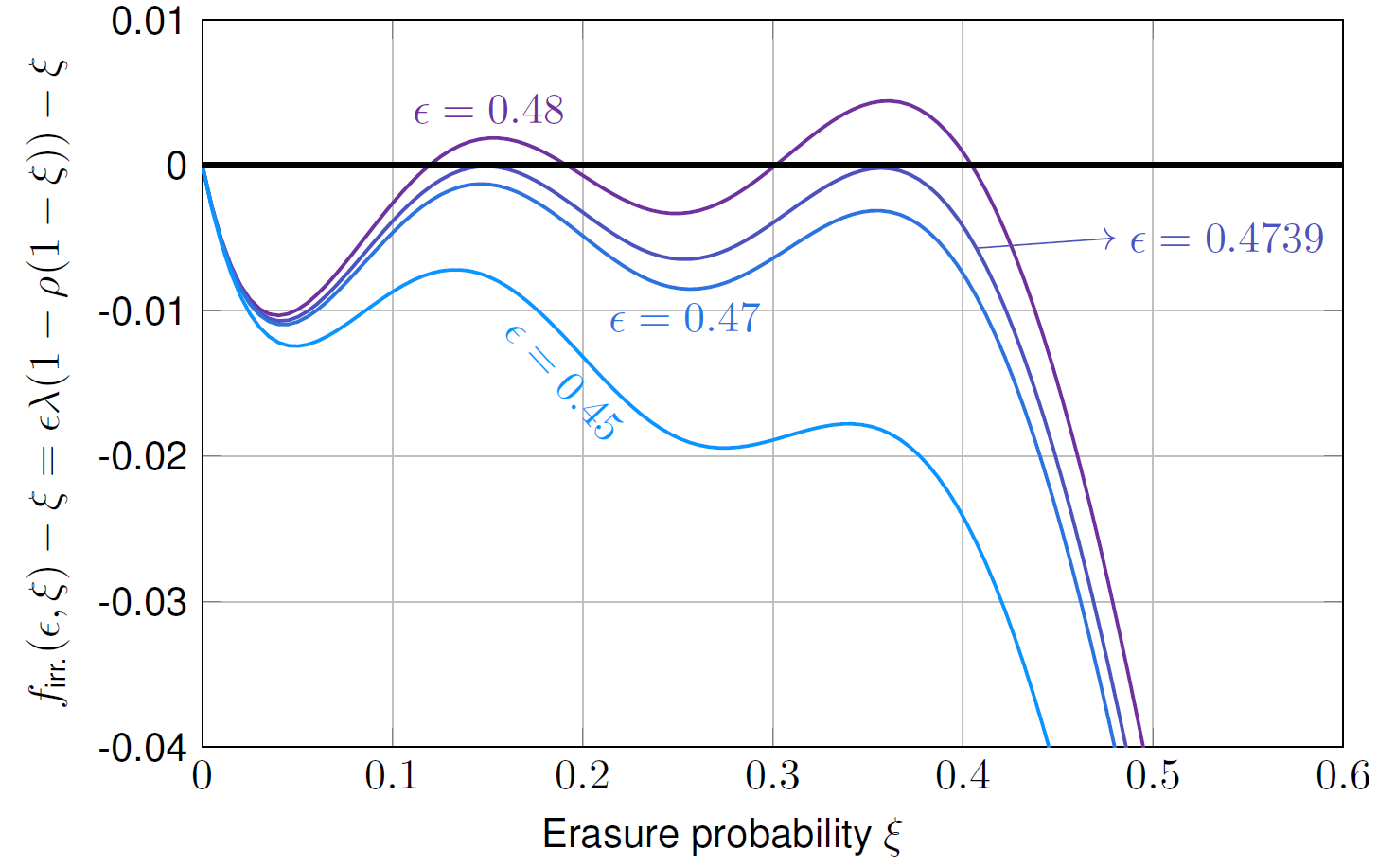
If the polynomial function is always negative (for a positive argument), the code can converge and we can formulate an optimization problem for code design, that is accompanied by a software tool to design codes yourself. For general channels, we resort to numerical methods and approximations to describe the evaluation of the messages that flow inside the decoder and to analyze converge, illustrated in the following figure:

Following the in-depth analysis of LDPC codes and deriving tools for optimizing codes, we define and introduce tools and methods to generate LDPC codes to be used in practice. We investigate how the codes shall be designed for different applications and look at structures that yield decoding errors and see tools on how to avoid such structures. At the end of the lecture, the participants will be able to design codes on their own to be used in practical systems.
Following the in-depth discussion of LDPC codes, we show recent developments in channel coding, namely spatially-coupled LDPC codes, which connect multiple LDPC codes in a well-defined way. An example of the Tanner graph of a spatially-coupled LDPC codes is shown in the following figure:  

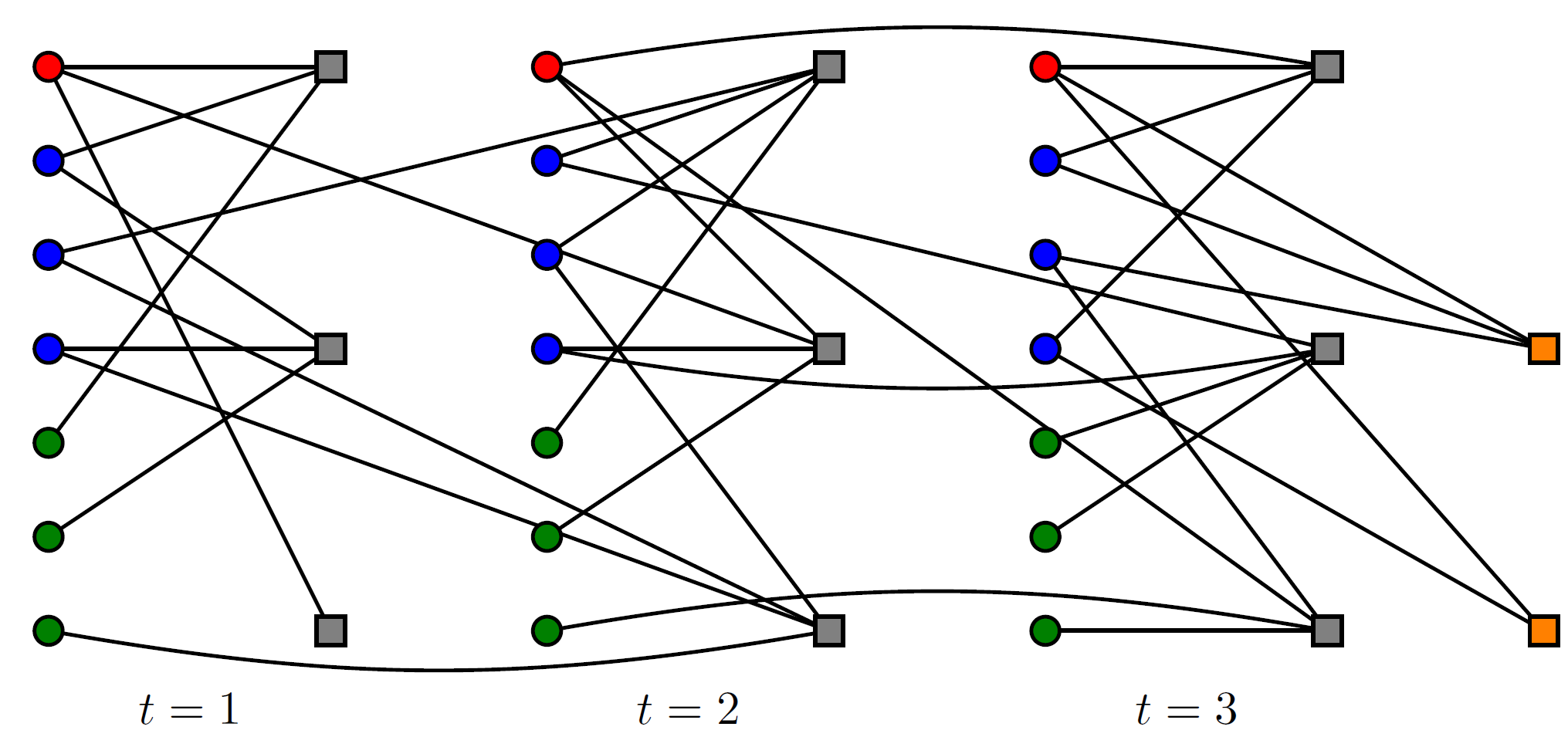
Spatially-coupled LDPC are a class of codes that can asymptotically achieve the channel capacity postulated by Shannon. We also introduce another modern class of channel code that are used for instance in the 5G mobile communication standard: polar codes. Polar codes are based on the Hadamard transform and can be very efficiently implemented and show extremely good performance at low error rates. The coding scheme based on an 8x8 Hadamard transform is shown in the following figure:

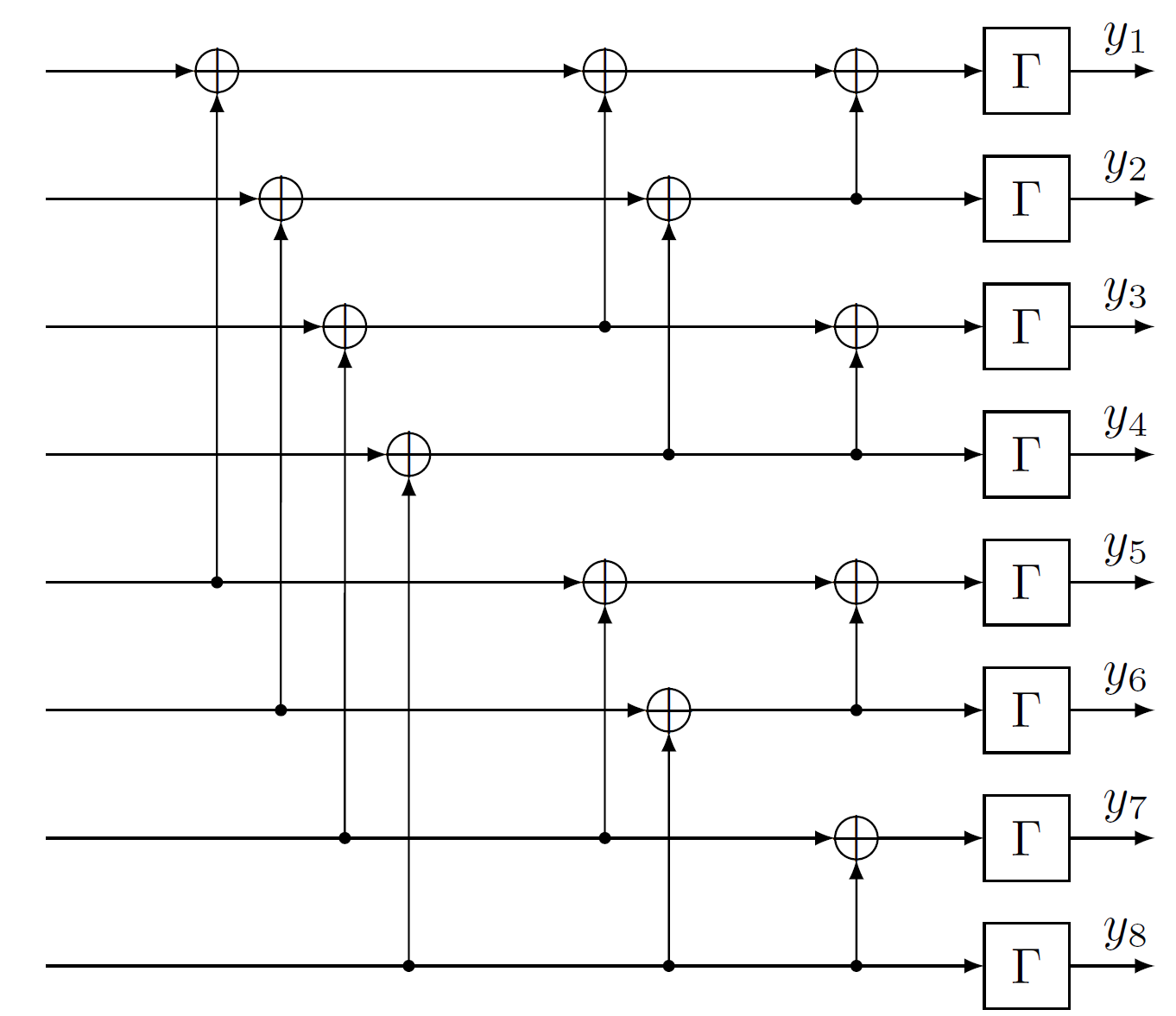
The lecture concludes with the discussion of both the design and decoders of Polar codes.