Machine Learning in Communications
In recent years, systems with the ability to learn drew wide attention in almost every field. Among many in the past decade, image and big data processing have been boosted tremendously by machine learning (ML)-based techniques, an artificial intelligence (AI) has beaten the world’s best chess or GO players, and specific neural networks are able to unfold proteins.
Traditional communication systems have managed to reach the fundamental limits of communications devised over 70 years ago by Claude Elwood Shannon, for some specific scenarios. However, for a large breadth of applications and scenarios, we either do not have sufficiently simple models enabling the design of optimal transmission systems or the resulting algorithm are prohibitively complex and computationally intense for low-power applications (e.g., Internet-of-Things, battery-driven receivers). The rise of machine learning and the advent of powerful computational resources have brought many novel potent numerical software tools, which enable the optimization of communication systems by reducing complexity or solving problems that could not be solved using traditional methods.
At the CEL, we carry out research on machine learning algorithms for optimization in communications. Basic work includes the model identification of a communication engineering problem, its conversion to an optimization problem and acquisition of data sets for training and evaluation. We are currently working on multiple projects, for example nonlinearity compensation in optical fiber communication systems, the design of novel modulation formats for short-reach optical communications, digital predistortion of nonlinear radio power amplifiers, blind channel estimation and equalization, and low-complexity channel decoding. In what follows, we will briefly describe some of these topics.
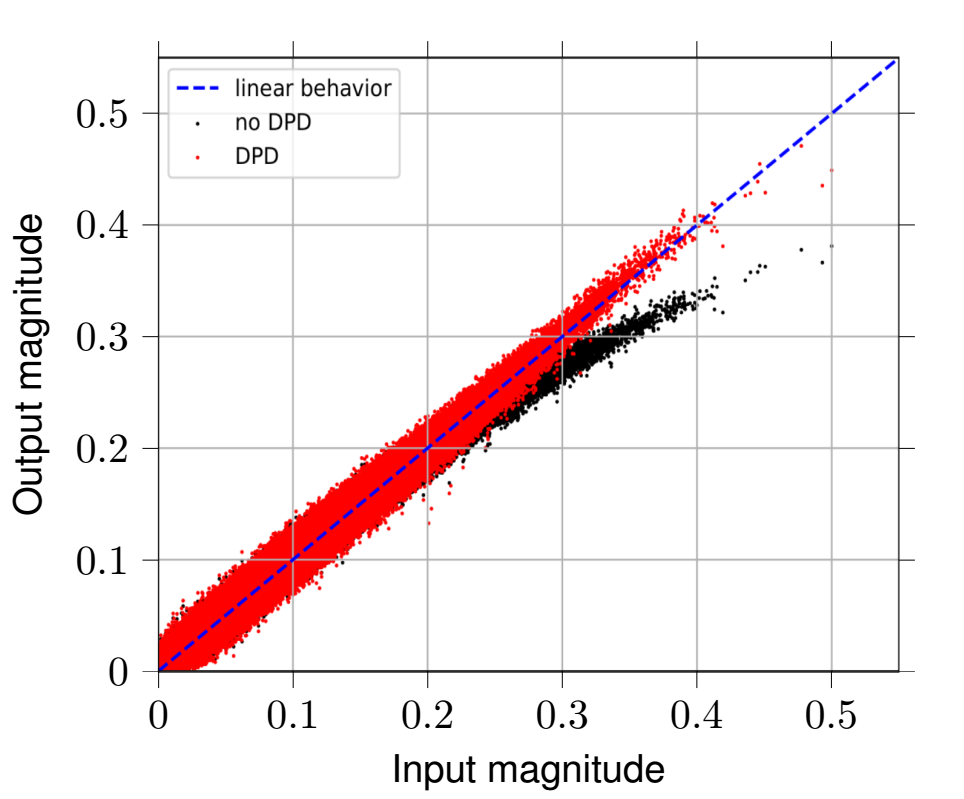
Combating the influence of system nonlinearities is an essential task not only, but especially in OFDM-systems, which inherently exhibit high Peak-to-Average Power Ratios (PAPR). This can drive radio power amplifiers into their nonlinear behavior, resulting in amplitude and phase distortions. Depending on the system bandwidth, the power amplifier introduces additional memory effects, which further degrades the system’s performance. In order to linearize the system, a Digital Predistortion (DPD) scheme can be designed and placed upstream the radio power amplifier. Unfortunately, higher bandwidths and cost-efficient radio power amplifiers intensify memory effects as well as amplitude and phase distortion, so conventional DPD (e.g., using Volterra series) are becoming exorbitantly complex and computationally intense. To overcome these issues, we designed a fast-adapting DPD based on feed-forward neural networks and tested the system using Software Defined Radios (SDRs). Figure 1 depicts the DPD’s performance for magnitude linearization. The predistorted time-domain OFDM-samples show linear behavior, whereas non-predistorted OFDM time-domain samples experience nonlinear distortion.
Commonly, channel equalization is conducted by non-blind adaptive algorithms which require known pilot symbols within the transmit sequence and, thus, lose data rate. Since communication systems become more and more optimized, there is a strong demand for blind equalizers which may approach maximum likelihood performance. Although there is a bunch of proposed schemes, basically there is only one applicable optimal algorithm for the special case of constant modulus (CM) modulation formats (e.g., M-PSK). Other schemes mainly suffer poor convergence rates, high implementation complexities, and sub-optimal criteria.
At the CEL, we analyze novel approaches based on unsupervised deep learning, which potentially approach maximum likelihood performance. Since its functionality differs from the classical digital signal processing (DSP) blocks, we have to develop metrics and environments for fair comparison. Also, some common ML issues, such as limited training sets, do not apply to communications, so adaptions may be reasonable.
For short channel codes, such as BCH, Reed-Muller and Polar codes, achieving close to maximum likelihood decoding performance using conventional methods is computationally complex. Fueled by the advances in the field of deep learning, belief propagation (BP) decoding can also be formulated in the context of deep neural networks. In BP decoding, messages are passed through unrolled iterations in a feed-forward fashion. Additionally, weights can be introduced
at the edges, which are then optimized using stochastic gradient descent (and variants thereof). This decoding method is commonly referred to as neural belief propagation and can be seen as a generalization of BP decoding, where all messages are scaled by a single damping coefficient. However, the weights add extra decoder complexity. Additionally, in order to achieve competitive performance, overcomplete parity-check matrices are necessary, which further increase decoding complexity. In our research [1], we have employed pruning techniques from ML to significantly reduce decoder complexity and have jointly optimized quantizers for the messages, such that the resulting decoders are directly ready for hardware implementation. The results are shown in Fig. 2, where we see that our optimized decoder operates within 0.5 dB from ML performance. More details can be found in [1].
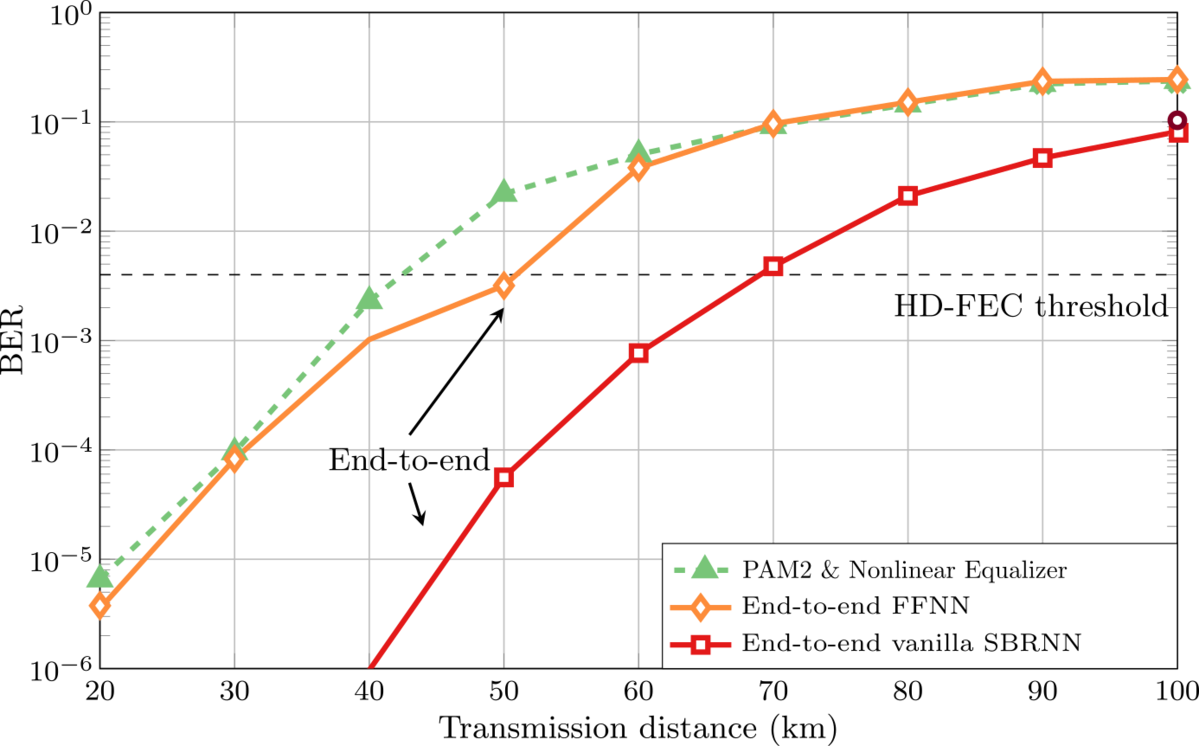
For the design of short-reach optical communication systems based on intensity modulation with direct detection (IM/DD), we may interpret the complete communication chain from the transmitter input to the receiver output as a single neural network and optimize its parameters yielding optimal end-to-end communication performance. In such systems, the combination of chromatic dispersion, introduced inter-symbol interference (ISI), and nonlinear signal detection by a photodiode imposes severe limitations. We have investigated multiple approaches for designing the neural networks [2], [3], including feed-forward and recurrent neural networks. We have shown experimentally that our networks can outperform pulse amplitude modulation (PAM) with conventional linear and nonlinear equalizers (e.g., based on Volterra filters). We have additionally employed Generative Adversarial Networks (GANs) to approximate experimental channels [4]. In Fig. 3, we exemplarily show the bit error rate performance of three such systems (conventional PAM with nonlinear equalizer and two different end-to-end optimized transceivers), where we can observe gains in the range of 20-25km at the FEC threshold.
References
[1] A. Buchberger, C. Häger, H. D. Pfister, L. Schmalen, and A. Graell i Amat, “Pruning Neural Belief Propagation Decoders,” IEEE International Symposium on Information Theory (ISIT), Los Angeles, CA, USA, Jun. 2020
[2] B. Karanov, M. Chagnon, F. Thouin, T. A. Eriksson, H. Bülow, D. Lavery, P. Payvel and L. Schmalen, “End-to-end Deep Learning of Optical Fiber Communications,” IEEE/OSA Journal of Lightwave Technology, vol. 36, no. 20, pp. 4843-4855, Oct. 2018, also available as arXiv:1804.04097
[3] B. Karanov, M. Chagnon, V. Aref, F. Ferreira, D. Lavery, P. Bayvel, and L. Schmalen, “Experimental Investigation of Deep Learning for Digital Signal Processing in Short Reach Optical Fiber Communications,” IEEE Workshop on Signal Processing Systems (SiPS), Coimbra, Portugal, Oct. 2020 (also available on https://arxiv.org/abs/2005.08790)
[4] B. Karanov, M. Chagnon, V. Aref, D. Lavery, P. Bayvel, and L. Schmalen, “Concept and Experimental Demonstration of Optical IM/DD End-to-End System Optimization using a Generative Model,” Optical Fiber Communications Conference (OFC), San Diego, CA, USA, paper Th2A.48, Mar. 2020